а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Спрятать решение
Решение.
а) Используем формулу синуса двойного угла, выносим за скобки:
б) Изображая корни на единичной окружности, находим, что отрезку принадлежат корни
и
Ответ:а) б)
Спрятать критерии
Критерии проверки:
| Критерии оценивания выполнения задания | Баллы |
|---|---|
| Обоснованно получены верные ответы в обоих пунктах. | 2 |
| Обоснованно получен верный ответ в пункте а),
ИЛИ получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б). |
1 |
| Решение не соответствует ни одному из критериев, перечисленных выше. | 0 |
| Максимальный балл | 2 |
Источник: ЕГЭ по математике — 2015. Досрочная волна, Запад.
Спрятать решение
·
·
Курс Д. Д. Гущина
·
Гость 07.03.2016 10:50
Здравствуйте. Хотелось бы спросить, почему вы в решении (x=…) используете одну переменную k? Разве переменные не должны отличаться?
Александр Иванов
В данном задании это не принципиально. Можно использовать одну и ту же букву, можно разные.
А бывают более сложные ситуации (системы уравнений, неравенства и т.п.) в них бывает, что обязательно разные буквы использовать, а бывает − обязательно одинаковые.
Решение 18 варианта ЕГЭ профильного уровня из сборника 36 вариантов Ященко 2023
Скачать сборник в pdf
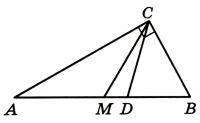
Угол между биссектрисой CD и медианой CM проведёнными из вершины прямого угла C треугольника ABC, равен 10°. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
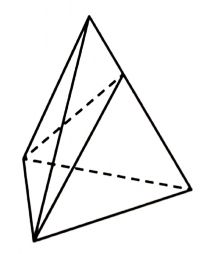
Объём треугольной пирамиды равен 14. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 2:5, считая от вершины пирамиды. Найдите больший из объёмов пирамид, на которые плоскость разбивает исходную пирамиду.
Перед началом первого тура чемпионата по шашкам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 шашистов, среди которых 4 спортсмена из России, в том числе Фёдор Волков. Найдите вероятность того, что в первом туре Фёдор Волков будет играть с каким-либо шашистом из России.
Игральный кубик бросили один или несколько раз. Оказалось, что сумма всех выпавших очков равна 3. Какова вероятность того, что было сделано два броска? Ответ округлите до сотых.
Найдите корень уравнения (log_4{2^{5x+7}}=3).
Найдите значение выражения (dfrac{a^{3{,}33}}{a^{2{,}11}cdot a^{2{,}22}}) при (a=dfrac{2}{7}).
Прямая (y=9x+6) является касательной к графику (y=ax^2-19x+13). Найдите (a).
Расстояние от наблюдателя, находящегося на высоте (h) м над землёй, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле (l=sqrt{dfrac{Rh}{500}}), где (R = 6400) км − радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 24 км?
Первый садовый насос перекачивает 10 литров воды за 5 минуты, второй насос перекачивает тот же объём воды за 7 минут. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 72 литров воды?
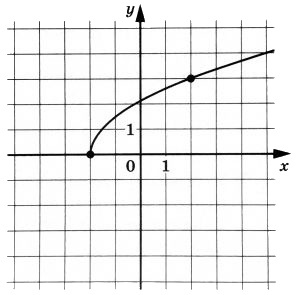
На рисунке изображен график функции (f(x)=ksqrt{x+p}). Найдите (f(0{,}25)).
Найдите наибольшее значение функции (y=2x^2-12x+8ln{x}-5) на отрезке (left[dfrac{12}{13};dfrac{14}{13}right]).
а) Решите уравнение (7cos{x}-4cos^3{x}=2sqrt{3}sin{2x}).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[-4pi;-3piright])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -4π | 18. -23π/6 | 19. -15π/4 | 20. -11π/3 |
| 21. -7π/2 | 22. -10π/3 | 23. -13π/4 | 24. -19π/6 |
| 25. -3π |
Основание пирамиды SABC — прямоугольный треугольник ABC с прямым углом при вершине C. Высота пирамиды проходит через точку B.
а) Докажите, что середина ребра SA равноудалена от вершин B и C.
б) Найдите угол между плоскостью SBC и прямой, проходящей через середины ребёр BC и SA, если известно, что BS=2AC.
Решите неравенство (log^2_{5}{left(x^4right)}-28log_{0{,}04}{left(x^2right)}leqslant 8).
Производство (x) тыс. единиц продуктции обходится в (q=3x^2+6x+13) млн рублей в год. При цене (p) тыс. рублей за единицу годовая прибыль от продажи этой продукции (в млн рублей) составляет (px-q). При каком наименьшем значении (p) через пять лет суммарная прибыль может составить не менее 70 млн рублей при некотором значении (x)?
Точки A1, B1, C1 — середины сторон соответственно BC, AC и AB остроугольного треугольника ABC.
а) Докажите, что окружности, описанные около треугольника A1CB1, A1BC1 и B1AC1 пересекаются в одной точке.
б) Известно, что AB=AC=17 и BC=16. Найдите радиус окружности, вписанной в треугольник, вершины которого — центры окружностей, описанных около треугольников A1CB1, A1BC1 и B1AC1.
Найдите все значения (a), при каждом из которых система уравнений (begin{cases} left(x-a+3right)^2+left(y+a-2right)^2=a+dfrac{7}{2}, x-y=a-1 end{cases})имеет единственное решение.
Для действительного числа (x) обозначим через (left[xright]) наибольшее целое число, не превосходящее (x). Например, (left[dfrac{11}{4}right]=2), так как (2leqslantdfrac{11}{4}<3).
а) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{9}right]=n)?
б) Существует ли такое натуральное число (n), что (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{5}right]=n+2)?
в) Сколько существует различных натуральных (n), для которых (left[dfrac{n}{2}right]+left[dfrac{n}{3}right]+left[dfrac{n}{8}right]+left[dfrac{n}{23}right]=n+2021)?
Введите ответ в форме строки «да;да;1234». Где ответы на пункты разделены «;», и первые два ответа с маленькой буквы.
Пробный тренировочный вариант №26 в формате решу ОГЭ 2023 по математике 9 класс от 7 марта 2023 года с ответами и решением по новой демоверсии ОГЭ 2023 года для подготовки на 100 баллов, задания взяты из открытого банка заданий ФИПИ и с экзамена прошлых лет, данный вариант вы можете решить онлайн или скачать.
Скачать тренировочный вариант и ответы
Посмотреть другие тренировочные варианты
variant_26_oge2023_matematika_9klass
Коля летом отдыхает у дедушки и бабушки в деревне Марьевке. Коля с дедушкой собираются съездить на велосипедах в село Сосновое на железнодорожную станцию. Из Марьевки в Сосновое можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе – через деревню Николаевку до деревни Запрудье, где нужно повернуть под прямым углом направо на другое шоссе, ведущее в Сосновое.
Есть и третий маршрут: в Николаевке можно свернуть на прямую тропинку, которая идёт мимо озера прямо в Сосновое. По шоссе Коля с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Марьевки до Николаевки равно 12 км, от Марьевки до Запрудья – 20 км, а от Запрудья до Соснового 15 км.
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
Ответ: 1432
2. На сколько процентов скорость, с которой едут Коля с дедушкой по тропинке, меньше их скорости по шоссе?
Ответ: 25
3. Сколько минут затратят на дорогу Коля с дедушкой, если поедут на станцию через Запрудье?
Ответ: 105
4. Найдите расстояние от д. Николаевка до с. Сосновое по прямой. Ответ дайте в километрах.
Ответ: 17
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответе укажите, сколько минут потратят на дорогу Коля с дедушкой, если поедут этим маршрутом.
Ответ: 100
6. Найдите значение выражения 4,4 − 1,7.
Ответ: 2,7
8. Найдите значение выражения (4𝑏) 2 : 𝑏 5 ∙ 𝑏 3 при 𝑏 = 128.
Ответ: 16
9. Найдите корень уравнения (𝑥 − 5) 2 = (𝑥 − 2 .
Ответ: 6, 5
10. В магазине канцтоваров продаётся 84 ручки, из них 22 красных, 9 зелёных, 41 фиолетовая, остальные синие и чёрные, их поровну. Найдите вероятность того, что случайно выбранная в этом магазине ручка будет красной или фиолетовой.
Ответ: 0, 75
11. На рисунках изображены графики функций вида 𝑦 = 𝑘𝑥 +𝑏. Установите соответствие между графиками функций и знаками коэффициентов 𝑘 и 𝑏. В таблице под каждой буквой укажите соответствующий номер.
Ответ: 312
12. Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой 𝑡𝐹 = 1,8𝑡𝐶 +32, где 𝑡𝐶 − температура в градусах Цельсия, 𝑡𝐹 − температура в градусах Фаренгейта. Скольким градусам по шкале Фаренгейта соответствует 80 градусов по шкале Цельсия?
Ответ: 176
13. Укажите решение неравенства −3 − 𝑥 ≥ 𝑥 −6.
Ответ: 1
14. Курс воздушных ванн начинают с 10 минут в первый день и увеличивают время этой процедуры в каждый следующий день на 10 минут. В какой по счёту день продолжительность процедуры достигнет 1 часа 20 минут?
Ответ: 8
15. Диагонали 𝐴𝐶 и 𝐵𝐷 параллелограмма 𝐴𝐵𝐶𝐷 пересекаются в точке 𝑂, 𝐴𝐶 = 12, 𝐵𝐷 = 20, 𝐴𝐵 = 7. Найдите 𝐷𝑂.
Ответ: 10
16. Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.
Ответ: 64
17. Найдите площадь квадрата, описанного около окружности радиуса 40.
Ответ: 6400
18. На клетчатой бумаге с размером клетки 1 × 1 изображена трапеция. Найдите длину её средней линии.
Ответ: 4
19. Какое из следующих утверждений верно?
1) Боковые стороны любой трапеции равны.
2) Серединные перпендикуляры к сторонам треугольника пересекаются в точке, являющейся центром окружности, описанной около треугольника.
3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.
Ответ: 2
20. Решите уравнение 𝑥(𝑥 2 + 2𝑥 + 1) = 2(𝑥 +1).
Ответ: -2; -1; 1
21. Свежие фрукты содержат 78% воды, а высушенные – 22%. Сколько сухих фруктов получится из 78 кг свежих фруктов?
Ответ: 22
23. Точки 𝑀 и 𝑁 являются серединами сторон 𝐴𝐵 и 𝐵𝐶 треугольника 𝐴𝐵𝐶 соответственно. Отрезки 𝐴𝑁 и 𝐶𝑀 пересекаются в точке 𝑂, 𝐴𝑁 = 27, 𝐶𝑀 = 18. Найдите 𝐶𝑂.
Ответ: 12
24. В трапеции 𝐴𝐵𝐶𝐷 с основаниями 𝐴𝐷 и 𝐵𝐶 диагонали пересекаются в точке 𝑂. Докажите, что площади треугольников 𝐴𝑂𝐵 и 𝐶𝑂𝐷 равны.
25. Боковые стороны 𝐴𝐵 и 𝐶𝐷 трапеции 𝐴𝐵𝐶𝐷 равны соответственно 40 и 41, а основание 𝐵𝐶 равно 16. Биссектриса угла 𝐴𝐷𝐶 проходит через середину стороны 𝐴𝐵. Найдите площадь трапеции.
Ответ: 820
Тренировочные варианты ОГЭ по математике 9 класс задания с ответами
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Public user contributions licensed under
cc-wiki license with attribution required
9 марта 2023
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой

9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika
Решу егэ математика профиль 509501
Задание 12 № 509501
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Используем формулу синуса двойного угла, выносим за скобки:
Б) Изображая корни на единичной окружности, находим, что отрезку принадлежат корни и
Здравствуйте. Хотелось бы спросить, почему вы в решении (x=. ) используете одну переменную k? Разве переменные не должны отличаться?
В данном задании это не принципиально. Можно использовать одну и ту же букву, можно разные.
А бывают более сложные ситуации (системы уравнений, неравенства и т. п.) в них бывает, что обязательно разные буквы использовать, а бывает − обязательно одинаковые.
Задание 12 № 509501
Используете одну переменную k.
Ege. sdamgia. ru
17.05.2019 23:51:10
2019-05-17 23:51:10
Источники:
Https://ege. sdamgia. ru/problem? id=509501
Решу егэ математика профиль 509501 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 501507
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
А) В силу нечетности и периодичности синуса имеем:
Б) При помощи числовой прямой или тригонометрической окружности (см. рис.) для каждой из задающих решения серий отберем корни уравнения, принадлежащие отрезку
Задание 12 № 501507
Б При помощи числовой прямой или тригонометрической окружности см.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 509501
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Используем формулу синуса двойного угла, выносим за скобки:
Б) Изображая корни на единичной окружности, находим, что отрезку принадлежат корни и
Здравствуйте. Хотелось бы спросить, почему вы в решении (x=. ) используете одну переменную k? Разве переменные не должны отличаться?
В данном задании это не принципиально. Можно использовать одну и ту же букву, можно разные.
А бывают более сложные ситуации (системы уравнений, неравенства и т. п.) в них бывает, что обязательно разные буквы использовать, а бывает − обязательно одинаковые.
Задание 12 № 509501
А Используем формулу синуса двойного угла, выносим за скобки.
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 511595
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Используем формулу синуса двойного угла, выносим за скобки:
Б) Изображая корни на единичной окружности, находим, что отрезку принадлежат корни
Источники:
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ математика профиль 509501
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Задание 12 № 509501
А) Решите уравнение
Б) Укажите корни этого уравнения, принадлежащие отрезку
А) Используем формулу синуса двойного угла, выносим за скобки:
Б) Изображая корни на единичной окружности, находим, что отрезку принадлежат корни и
Здравствуйте. Хотелось бы спросить, почему вы в решении (x=. ) используете одну переменную k? Разве переменные не должны отличаться?
В данном задании это не принципиально. Можно использовать одну и ту же букву, можно разные.
А бывают более сложные ситуации (системы уравнений, неравенства и т. п.) в них бывает, что обязательно разные буквы использовать, а бывает − обязательно одинаковые.
Задание 12 № 509501
А Используем формулу синуса двойного угла, выносим за скобки.
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Dankonoy. com
12.06.2020 15:22:46
2020-06-12 15:22:46
Источники:
Https://dankonoy. com/ege/ege12/archives/4548
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Решу егэ математика профиль 509501
Задание 7 № 42829
В ходе распада радиоактивного изотопа его масса уменьшается по закону где − начальная масса изотопа, T − время, прошедшее от начального момента, T − период полураспада. В начальный момент времени масса изотопа 68 мг. Период его полураспада составляет 5 мин. Найдите, через сколько минут масса изотопа будет равна 17 мг.
Это задание ещё не решено, приводим решение прототипа.
В ходе распада радиоактивного изотопа его масса уменьшается по закону где — начальная масса изотопа, T — время, прошедшее от начального момента, T — период полураспада. В начальный момент времени масса изотопа 40 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.
Задача сводится к решению уравнения при заданных значениях параметров мг и мин:
Приведем решение Ильи Князева.
За каждый период полураспада T = T масса изотопа уменьшается вдвое. Следовательно, за первый период масса уменьшилась с 40 мг до 20 мг, за второй период с 20 мг до 10 мг, за третий период с 10 мг до 5 мг. Всего прошло три периода полураспада или 30 минут.
Задание 7 № 42829
Найдите, через сколько минут масса изотопа будет равна 5 мг.
Reshuege. ru
16.06.2019 22:48:39
2019-06-16 22:48:39
Источники:
Https://reshuege. ru/problem? id=42829
Цена: 401 руб.
товар в наличии
ЕГЭ. Математика. Функции, заданные графиками, и их производные. Задача 7, профильный уровень, задача 7, базовый уровень. Рабочая тетрадь.
Рабочая тетрадь по математике серии «ЕГЭ. Математика» ориентирована на подготовку учащихся старшей школы к успешной сдаче Единого государственного экзамена по математике по базовому и профильному уровням. В рабочей тетради представлены задачи по одной позиции контрольных измерительных материалов.
На различных этапах обучения пособие поможет обеспечить уровневый подход к организации повторения, осуществить контроль и самоконтроль знаний по задачам, посвящённым геометрическому смыслу производной. Рабочая тетрадь ориентирована на один учебный год, однако при необходимости позволит в кратчайшие сроки восполнить пробелы в знаниях выпускника.
Тетрадь предназначена для учащихся старшей школы, учителей математики, родителей.
Издание соответствует Федеральному государственному образовательному стандарту (ФГОС).
- ЕГЭ по математике
- Производитель: МЦНМО
- Продавец: официальный сайт Лабиринт
- Артикул: 934752
Доставка Почтой России, экспресс-доставка курьером или заказ забирается самовывозом из пунктов выдачи и постаматов. Успей купить по дешевой цене, товар находится в ограниченной продаже!
Цена актуальна на дату: 05.03.2023 г. Предложение по артикулу 934752 не является публичной офертой. Для покупки перейдите в интернет-магазин по ссылке «Купить» или «Заказать», добавьте товар в корзину и оформите заказ.
Доставка
- Курьером;
- Самовывоз из постаматов и пунктов выдачи;
- Почтой России;
- Транспортными компаниями.
Оплата
- Наличными при получении;
- Банковской картой;
- Безналичным расчетом.
* Варианты доставки и оплаты могут отличаться.
Ранее, счета за холодную воду приходили отдельно от других коммунальных услуг.
В Санкт-Петербурге было внесено изменение в систему оплаты коммунальных услуг, и теперь жители могут оплачивать свои счета за холодную воду в рамках единой квитанции за ЖКУ. Ранее, счета за холодную воду приходили отдельно от других коммунальных услуг, что иногда приводило к затруднениям и путанице у жителей города.
Это изменение внесено с целью упростить процесс оплаты коммунальных услуг и уменьшить количество счетов, которые должны получать жители. В настоящее время, жители Санкт-Петербурга могут оплачивать все свои коммунальные счета в одной единой квитанции, что существенно облегчает процесс оплаты и снижает вероятность ошибок.
Также, это изменение поможет уменьшить количество неплатежей за коммунальные услуги, так как жители смогут лучше контролировать свои расходы на ЖКУ и, возможно, смогут легче оплачивать свои счета вовремя. В целом, внедрение единой квитанции за ЖКУ в Санкт-Петербурге является положительным шагом в упрощении и улучшении процесса оплаты коммунальных услуг для жителей города.
#Марина Цурикова#2#Общество#Город и горожане