509412 математика егэ
Задание 2 № 509412
У Вити в копилке лежит 12 рублёвых, 6 двухрублёвых, 4 пятирублёвых и 3 десятирублёвых монеты. Витя наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
У Вити в копилке лежит 12 + 6 + 4 + 3 = 25 монет на сумму 12 + 12 + 20 + 30 = 74 рубля. Больше 70 рублей останется, если достать из копилки либо рублёвую, либо двухрублёвую монету. Таких монет 12 + 6 = 18. Искомая вероятность равна 18 : 25 = 0,72.
Задание 2 № 509412
Найдите вероятность того, что оставшаяся в копилке сумма составит более 70 рублей.
Math-ege. sdamgia. ru
25.02.2018 9:29:25
2018-02-25 09:29:25
Источники:
Https://math-ege. sdamgia. ru/problem? id=509412
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 509412 математика егэ
509412 математика егэ
509412 математика егэ
Задание 2 № 509433
У Дины в копилке лежит 7 рублёвых, 5 двухрублёвых, 6 пятирублёвых и 2 десятирублёвых монеты. Дина наугад достаёт из копилки одну монету. Найдите вероятность того, что оставшаяся в копилке сумма составит менее 60 рублей.
У Дины в копилке лежит 7 + 5 + 6 + 2 = 20 монет на сумму 7 + 10 + 30 + 20 = 67 рублей. Менее 60 рублей останется, если достать из копилки десятирублёвую монету. Искомая вероятность равна 2 : 20 = 0,1.
Задание 2 № 509433
509412 математика егэ.
Ege. sdamgia. ru
04.07.2017 10:55:10
2017-07-04 10:55:10
Источники:
Https://ege. sdamgia. ru/test? likes=509412
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } 509412 математика егэ
509412 математика егэ
509412 математика егэ
А) Решите уравнение
Б) Найдите все корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка C1, причём CC1 — образующая цилиндра, а AC — диаметр основания. Известно, что
А) Докажите, что угол между прямыми и BC равен
Б) Найдите объём цилиндра.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15-го января планируется взять кредит в банке на сумму 2,4 млн рублей на 24 месяца. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 3% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Какую сумму нужно выплатить банку в первые 12 месяцев?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Дана трапеция с диагоналями равными 8 и 15. Сумма оснований равна 17.
А) Докажите, что диагонали перпендикулярны.
Б) Найдите площадь трапеции.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Найдите все значения A, при которых уравнение
Имеет ровно два различных корня.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
На конкурсе «Мисс−261» выступление каждой участницы оценивают шесть судей. Каждый судья выставляет оценку — целое число баллов от 0 до 10 включительно. Известно, что за выступление участницы С все члены жюри выставили различные оценки. По старой системе оценивания итоговый балл за выступление определяется как среднее арифметическое всех оценок судей. По новой системе оценивания итоговый балл вычисляется следующим образом: отбрасываются две наибольшие оценки, и считается среднее арифметическое четырех оставшихся оценок.
А) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной 18?
Б) Может ли разность итоговых баллов, вычисленных по старой и новой системам оценивания, быть равной
В) Найдите наименьшее возможное значение разности итоговых баллов, вычисленных по старой и новой системам оценивания.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
На следующей странице вам будет предложено проверить их самостоятельно.
Math-ege. sdamgia. ru
11.04.2018 21:52:23
2018-04-11 21:52:23
Источники:
Https://math-ege. sdamgia. ru/test? id=44902083
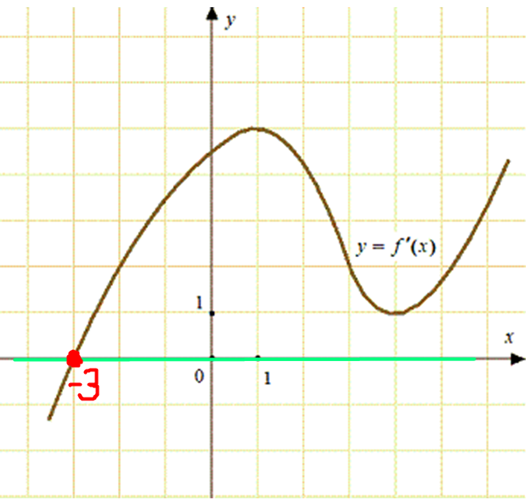
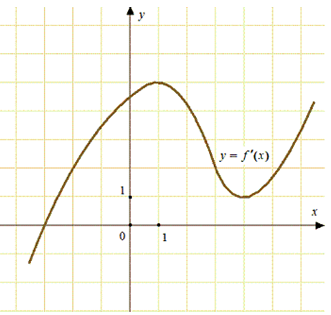
ЕГЭ профильный уровень. №7 Геометрический смысл производной, касательная. Задача 11
ОТВЕТ: — 3.
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, то её угловой коэффициент равен 0 (коэффициент перед x). Следовательно, необходимо найти точку, в которых (f’left( {{x_0}} right) = 0). Этому соответствует точка пересечения графика производной с прямой (y = 0) (ось Ox). Это точка –3 (выделена красным цветом см. рисунок).
Ответ: –3.
Комментарии для сайта Cackle
9 марта 2023
В закладки
Обсудить
Жалоба
Теория и практика.
Содержание
1) Прямые
2) Параболы
3) Как искать пересечение параболы и прямой, двух парабол
4) Гипербола. Асимптотические точки гиперболы
5) Пересечение гиперболы и прямой
6) Иррациональные функции
7) Пересечение корня и прямой

9) Показательные функции
10) Логарифмические функции
10_zadacha.pdf
Источник: vk.com/profimatika
Вариант МА2210301 и ответы
Скачать ответы и
решения для вариантов
1.
Каждый день во время конференции расходуется 60 пакетиковчая.
Конференция длится 9 дней. В пачке чая 50 пакетиков. Какого наименьшего
количества пачек чая хватит на все дни конференции?
2.
Установите соответствие между величинами и их
возможнымизначениями: к каждому элементу первого столбца подберите
соответствующий элемент из второго столбца.
3.
В таблице показано расписание пригородных электропоездовпо
направлению Москва Курская – Крутое – Петушки. Владислав пришёл на станцию
Москва Курская в 18:20 и хочет уехать в Петушки на электропоезде без пересадок.
Найдите номер ближайшего электропоезда, который ему подходит.
5. В коробке вперемешку лежат чайные пакетики с
чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 4
раза больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно
выбранный из этой коробки пакетик окажется пакетиком с чёрным чаем.
8.
Некоторые учащиеся 10-х классов школы ходили в апреле наспектакль
«Гроза». В мае некоторые десятиклассники пойдут на постановку по пьесе
«Бесприданница», причём среди них не будет тех, кто ходил в апреле на спектакль
«Гроза». Выберите утверждения, которые будут верны при указанных условиях
независимо от того, кто из десятиклассников пойдёт на постановку по пьесе
«Бесприданница».
●
1) Каждый учащийся 10-х классов, который не ходил на спектакль
«Гроза», пойдёт на постановку по пьесе «Бесприданница».
●
2) Нет ни одного десятиклассника, который ходил на спектакль
«Гроза» и пойдёт на постановку по пьесе «Бесприданница».
●
3) Среди учащихся 10-х классов этой школы, которые не пойдут на
постановку по пьесе «Бесприданница», есть хотя бы один, который ходил на
спектакль «Гроза».
●
4) Найдётся десятиклассник, который не ходил на спектакль «Гроза»
и не пойдёт на постановку по пьесе «Бесприданница».
9.
На фрагменте географической карты схематично изображеныграницы
деревни Покровское и очертания озёр (площадь одной клетки равна одному
гектару). Оцените приближённо площадь озера Малого. Ответ дайте в гектарах с
округлением до целого значения.
10.
Диагональ прямоугольного экрана ноутбука равна 40 см, аширина
экрана ― 32 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
11.
Пирамида Снофру имеет форму правильной четырёхугольнойпирамиды,
сторона основания которой равна 220 м, а высота — 104 м. Сторона основания
точной музейной копии этой пирамиды равна 55 см. Найдите высоту музейной копии.
Ответ дайте в сантиметрах.
12.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°
, угол ABC равен 106° . Найдите угол ACB . Ответ дайте в градусах.
13.
Даны два цилиндра. Радиус основания и высота первогоцилиндра
равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго
цилиндра больше объёма первого?
15. В школе мальчики составляют 55 % от числа всех
учащихся. Сколько в этой школе мальчиков, если их на 50 человек больше, чем
девочек?
19.
Цифры четырёхзначного числа, кратного 5, записали вобратном
порядке и получили второе четырёхзначное число. Затем из исходного числа вычли
второе и получили 3366. В ответе укажите какое-нибудь одно такое исходное
число.
20.
Имеется два сплава. Первый содержит 45 % никеля, второй —5 %
никеля. Из этих двух сплавов получили третий сплав, содержащий 15 % никеля.
Масса первого сплава равна 40 кг. На сколько килограммов масса первого сплава
была меньше массы второго?
21.
Прямоугольник разбит на четыре меньших прямоугольникадвумя
прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и
далее по часовой стрелке, равны 2, 3 и 18. Найдите периметр четвёртого
прямоугольника.
Вариант МА2210305 и ответы
Скачать ответы и
решения для вариантов
1. Для покраски 1 кв. м потолка требуется 230 г
краски. Краска продаётся в банках по 2 кг. Какое наименьшее количество банок
краски нужно для покраски потолка площадью 44 кв. м?
3. В таблице представлены налоговые ставки на
автомобили в Москве с 1 января 2013 года. Какова налоговая ставка (в рублях за
1 л. с. в год) на автомобиль мощностью 115 л. с.?
5.
Помещение освещается двумя лампами. Вероятностьперегорания одной
лампы в течение года равна 0,3. Найдите вероятность того, что в течение года
обе лампы перегорят.
6.
В таблице даны результаты олимпиад по русскому языку ибиологии в
9 «А» классе. Похвальные грамоты дают тем школьникам, у кого суммарный балл по
двум олимпиадам больше 110 или хотя бы по одному предмету набрано не меньше 60
баллов. Укажите номера учащихся 9 «А» класса, набравших меньше 60 баллов по
русскому языку и получивших похвальные грамоты, без пробелов, запятых и других
дополнительных символов.
7.
На рисунке изображены график функции и касательные,проведённые к
нему в точках с абсциссами A, B, C и D. В правом столбце указаны значения
производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в
соответствие каждой точке значение производной функции в ней.
8.
Некоторые учащиеся 10-х классов школы ходили в ноябре наоперу
«Евгений Онегин». В марте некоторые десятиклассники пойдут на оперу «Руслан и
Людмила», причём среди них не будет тех, кто ходил в ноябре на оперу «Евгений
Онегин». Выберите утверждения, которые будут верны при указанных условиях независимо
от того, кто из десятиклассников пойдёт на оперу «Руслан и Людмила».
●
1) Каждый учащийся 10-х классов, который не ходил на оперу
«Евгений Онегин», пойдёт на оперу «Руслан и Людмила».
●
2) Нет ни одного десятиклассника, который ходил на оперу «Евгений
Онегин» и пойдёт на оперу «Руслан и Людмила».
●
3) Найдётся десятиклассник, который не ходил на оперу
«Евгений Онегин» и не пойдёт на оперу «Руслан и
Людмила».
●
4) Среди учащихся 10-х классов этой школы, которые не пойдут на
оперу «Руслан и Людмила», есть хотя бы один, который ходил на оперу «Евгений
Онегин».
9.
План местности разбит на клетки. Каждая клетка обозначаетквадрат
1м×1м . Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных
метрах.
10.
Пожарную лестницу длиной 10 м приставили к окну дома.Нижний конец
лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец
лестницы? Ответ дайте в метрах.
11.
Прямолинейный участок трубы длиной 4 м, имеющей всечении
окружность, необходимо покрасить снаружи (торцы трубы открыты, их красить не
нужно). Найдите площадь поверхности, которую необходимо покрасить, если внешний
обхват трубы равен 19 см. Ответ дайте в квадратных сантиметрах.
12.
В треугольнике ABC стороны AC и BC равны. Внешний угол при
вершине B равен 146° . Найдите угол C. Ответ дайте в градусах.
13.
Даны два шара радиусами 4 и 2. Во сколько раз объёмбольшего шара
больше объёма меньшего?
15. Число больных гриппом в школе уменьшилось за
месяц в пять раз. На сколько процентов уменьшилось число больных гриппом?
19.
Найдите пятизначное число, кратное 15, любые две соседниецифры
которого отличаются на 3. В ответе укажите какое-нибудь одно такое число.
20.
Теплоход, скорость которого в неподвижной воде равна 19 км/ч,
проходит по течению реки и после стоянки возвращается в исходный пункт.
Скорость течения равна 3 км/ч, стоянка длится 5 часов, а в исходный пункт
теплоход возвращается через 43 часа после отправления из него. Сколько
километров проходит теплоход за весь рейс?
21.
На кольцевой дороге расположены четыре бензоколонки: А, Б,В и Г.
Расстояние между А и Б — 55 км, между А и В — 40 км, между В и Г — 40 км, между
Г и А — 30 км (все расстояния измеряются вдоль кольцевой дороги по кратчайшей
дуге). Найдите расстояние (в километрах) между Б и В.
Вариант МА2210309 и ответы
Скачать ответы и
решения для вариантов
2.
Прямоугольный параллелепипед описан около цилиндра,радиус
основания которого равен 2. Объём параллелепипеда равен 3,2. Найдите высоту
цилиндра.
3.
В группе 16 человек, среди них — Анна и Татьяна. Группуслучайным
образом делят на 4 одинаковые по численности подгруппы. Найдите вероятность
того, что Анна и Татьяна окажутся в одной подгруппе.
4.
Агрофирма закупает куриные яйца только в двух домашниххозяйствах.
Известно, что 40 % яиц из первого хозяйства — яйца высшей категории, а из
второго хозяйства — 60 % яиц высшей категории. В этой агрофирме 50 % яиц высшей
категории. Найдите вероятность того, что яйцо, купленное у этой агрофирмы,
окажется из первого хозяйства.
9. Пристани A и B расположены на озере, расстояние
между ними равно 280 км. Баржа отправилась с постоянной скоростью из A в B. На
следующий день после прибытия она отправилась обратно со скоростью на 4 км/ч
больше прежней, сделав по пути остановку на 8 часов. В результате она затратила
на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость
баржи на пути из A в B. Ответ дайте в км/ч.
13. Основанием правильной пирамиды PABCD является
квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD
перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра
пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если AB
= 30.
15.
По вкладу «А» банк в конце каждого года планируетувеличивать на
13 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать
эту сумму на 7 % в первый год и на целое число n процентов за второй год.
Найдите наименьшее значение n , при котором за два года хранения вклад «Б»
окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16.
В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M
. Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б)
Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 22 .
18. У Ани есть 800 рублей. Ей нужно купить конверты
(большие и маленькие). Большой конверт стоит 32 рубля, а маленький — 25 рублей.
При этом число маленьких конвертов не должно отличаться от числа больших
конвертов больше чем на пять. а) Может ли Аня купить 24 конверта? б) Может ли
Аня купить 29 конвертов? в) Какое наибольшее число конвертов может купить Аня?
Вариант МА2210311 и ответы
Скачать ответы и
решения для вариантов
1.
Найдите периметр прямоугольника, если его площадь равна 12,а
отношение соседних сторон равно 1:3.
2.
Шар вписан в цилиндр. Площадь полной поверхностицилиндра равна
78. Найдите площадь поверхности шара.
3.
В магазине в среднем из 120 сумок 15 имеют скрытые
дефекты.Найдите вероятность того, что выбранная в магазине сумка окажется со
скрытыми дефектами.
4.
Игральный кубик бросают дважды. Известно, что в суммевыпало 11
очков. Найдите вероятность того, что во второй раз выпало 5 очков.
9. Игорь и Паша, работая вместе, могут покрасить
забор за 40 часов. Паша и Володя, работая вместе, могут покрасить этот же забор
за 48 часов, а Володя и Игорь, работая вместе, — за 60 часов. За сколько часов
мальчики покрасят забор, работая втроём?
13. Основанием правильной пирамиды PABCD является
квадрат ABCD . Сечение пирамиды проходит через вершину В и середину ребра PD
перпендикулярно этому ребру. а) Докажите, что угол наклона бокового ребра
пирамиды к её основанию равен 60° . б) Найдите площадь сечения пирамиды, если
AB = 24 .
15.
По вкладу «А» банк в конце каждого года планируетувеличивать на
11 % сумму, имеющуюся на вкладе в начале года, а по вкладу «Б» — увеличивать
эту сумму на 7 % в первый год и на целое число n процентов за второй год.
Найдите наименьшее значение n , при котором за два года хранения вклад «Б»
окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
16.
В треугольнике ABC медианы AA1 , BB1 и CC1 пересекаются в точке M
. Известно, что AC MB = 3 . а) Докажите, что треугольник ABC прямоугольный. б)
Найдите сумму квадратов медиан AA1 и CC1, если известно, что AC = 18.
18. У Ани есть 400 рублей. Ей нужно купить конверты
(большие и маленькие). Большой конверт стоит 22 рубля, а маленький — 17 рублей.
При этом число маленьких конвертов не должно отличаться от числа больших
конвертов больше чем на пять. а) Может ли Аня купить 19 конвертов? б) Может ли
Аня купить 23 конверта? в) Какое наибольшее число конвертов может купить Аня?
Скачать ответы и
решения для вариантов